Appearance
HyperLogLog
Business Problem Overview
Before we begin this section, let's consider a common business problem: if you're responsible for developing and maintaining a large website, and one day the boss asks the product manager for the UV data of each webpage on a daily basis, how would you implement this statistics module?
Counting PV Data
Counting PV (Page Views) is straightforward. You can assign an independent Redis counter to each webpage, with the key suffixed by the current date. Each request would trigger an incrby operation, allowing you to accumulate all PV data easily.
Counting UV Data
However, counting UV (Unique Visitors) is different; it requires deduplication. Multiple visits by the same user within a day should only count once. This means each webpage request must include the user's ID, whether the user is logged in or not, to ensure a unique identifier.
Simple Solution
You might already think of a simple solution: create an independent set for each page to store all user IDs that visited that page on the given day. When a request comes in, you can use sadd to add the user ID. By using scard, you can retrieve the size of this set, which gives you the UV data for that page. Indeed, this is a very straightforward solution.
Storage Limitations
However, if your page experiences very high traffic—like tens of millions of UVs—you'll need a very large set to maintain statistics, which can waste a lot of space. If many such pages exist, the storage requirements can be staggering. Is it worth consuming so much storage just for this deduplication feature? In fact, the data the boss needs doesn’t have to be too precise; the difference between 1.05 million and 1.06 million isn't significant. So, is there a better solution?
Introducing HyperLogLog
This section introduces a solution: Redis provides the HyperLogLog data structure to address such statistical problems. HyperLogLog offers an approximate deduplication counting method. While not precise, the standard error is only 0.81%, which is sufficient for the UV statistics requirement mentioned earlier.
HyperLogLog Usage
HyperLogLog is an advanced data structure in Redis that is quite useful, yet surprisingly underused by those familiar with it.
It provides two commands: pfadd and pfcount. Their meanings are quite straightforward—one for incrementing the count and the other for retrieving the count. The usage of pfadd is similar to the sadd command for sets; whenever a user ID comes in, you just add it. The usage of pfcount is akin to scard, allowing you to directly obtain the count.
plaintext
127.0.0.1:6379> pfadd codehole user1
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 1
127.0.0.1:6379> pfadd codehole user2
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 2
127.0.0.1:6379> pfadd codehole user3
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 3
127.0.0.1:6379> pfadd codehole user4
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 4
127.0.0.1:6379> pfadd codehole user5
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 5
127.0.0.1:6379> pfadd codehole user6
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 6
127.0.0.1:6379> pfadd codehole user7 user8 user9 user10
(integer) 1
127.0.0.1:6379> pfcount codehole
(integer) 10After a simple test, we find it quite accurate—there’s no discrepancy. Next, we’ll use a script to add more data and see if it remains accurate; if not, we’ll check how significant the discrepancy is. Life is short, so I’ll use Python! Let’s get the Python script running! 😄
python
# coding: utf-8
import redis
client = redis.StrictRedis()
for i in range(1000):
client.pfadd("codehole", "user%d" % i)
total = client.pfcount("codehole")
if total != i + 1:
print(total, i + 1)
breakOf course, Java works well too, with similar logic. Here’s the Java version:
java
public class PfTest {
public static void main(String[] args) {
Jedis jedis = new Jedis();
for (int i = 0; i < 1000; i++) {
jedis.pfadd("codehole", "user" + i);
long total = jedis.pfcount("codehole");
if (total != i + 1) {
System.out.printf("%d %d\n", total, i + 1);
break;
}
}
jedis.close();
}
}Observing Outputs
Let’s check the output:
plaintext
> python pftest.py
99 100When we add the 100th element, the results start to show inconsistencies. Next, let's increase the data to 100,000 and see how significant the total discrepancy is.
python
# coding: utf-8
import redis
client = redis.StrictRedis()
for i in range(100000):
client.pfadd("codehole", "user%d" % i)
print(100000, client.pfcount("codehole"))Java version:
java
public class JedisTest {
public static void main(String[] args) {
Jedis jedis = new Jedis();
for (int i = 0; i < 100000; i++) {
jedis.pfadd("codehole", "user" + i);
}
long total = jedis.pfcount("codehole");
System.out.printf("%d %d\n", 100000, total);
jedis.close();
}
}After running for about half a minute, we observe the output:
plaintext
> python pftest.py
100000 99723There’s a discrepancy of 277, which translates to a percentage error of 0.277%. For the above UV statistics requirement, this error rate is acceptable. We can run the previous script again, essentially adding the data a second time, and check the output. We’ll find that the pfcount result remains unchanged at 99723, indicating that it indeed possesses deduplication functionality.
Meaning of pfadd
What does the "pf" in pfadd mean? It stands for the initials of Philippe Flajolet, the inventor of the HyperLogLog data structure. The professor’s hairstyle was cool, giving him a laid-back vibe.
When to Use pfmerge
Besides pfadd and pfcount, HyperLogLog also provides a third command, pfmerge, which is used to combine multiple pf counts into a new pf value.
For instance, if we have two similar pages on a website and the operations team requests to merge the data for these two pages, including their UV visit counts, pfmerge would come in handy.
Important Considerations
The HyperLogLog data structure is not free. While using it doesn’t incur costs, it does occupy a certain storage space of about 12 KB. Therefore, it’s not suitable for counting data related to individual users. If you have millions of users, the storage costs can be staggering. However, compared to set storage solutions, the space used by HyperLogLog can be described as very minimal in contrast.
You don’t need to worry too much, as Redis has optimized storage for HyperLogLog. When the count is small, it uses sparse matrix storage, occupying very little space. Only as the count grows does it convert to a dense matrix, which then occupies 12 KB of space once the sparse matrix exceeds a threshold.
HyperLogLog Implementation Principle
While the usage of HyperLogLog is straightforward, its underlying implementation is quite complex. If you’re not particularly interested, you can skip this section for now.
To help understand the internal workings of HyperLogLog, I’ve created the following illustration.
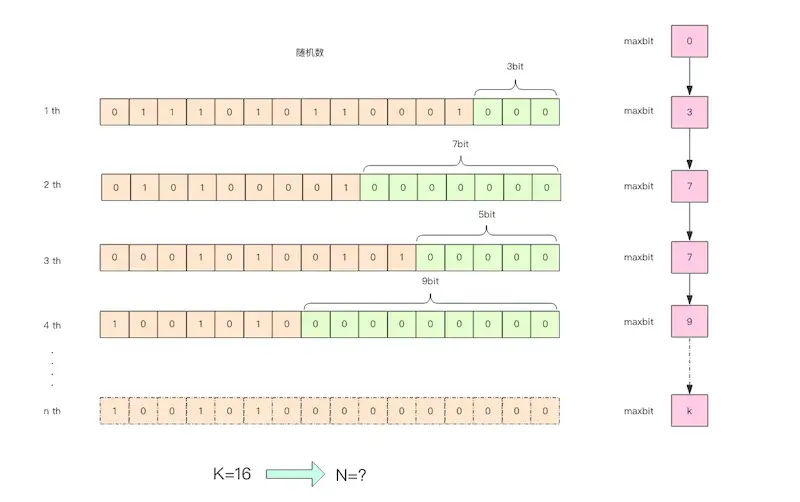
The idea is to observe a series of random integers and record the maximum length ( k ) of consecutive low bits that are zero. This ( k ) value can be used to estimate the count of random numbers. First, let’s write some code to experiment with the relationship between the number of random integers and the ( k ) value.
python
import math
import random
# Count low zeros
def low_zeros(value):
for i in range(1, 32):
if value >> i << i != value:
break
return i - 1
# Class to keep track of maximum low zeros
class BitKeeper:
def __init__(self):
self.maxbits = 0
def random(self):
value = random.randint(0, 2**32 - 1)
bits = low_zeros(value)
if bits > self.maxbits:
self.maxbits = bits
class Experiment:
def __init__(self, n):
self.n = n
self.keeper = BitKeeper()
def do(self):
for _ in range(self.n):
self.keeper.random()
def debug(self):
print(self.n, '%.2f' % math.log(self.n, 2), self.keeper.maxbits)
for i in range(1000, 100000, 100):
exp = Experiment(i)
exp.do()
exp.debug()Java Version
Here's the equivalent Java implementation:
java
import java.util.concurrent.ThreadLocalRandom;
public class PfTest {
static class BitKeeper {
private int maxbits;
public void random() {
long value = ThreadLocalRandom.current().nextLong(1L << 32);
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
}
}
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
private int n;
private BitKeeper keeper;
public Experiment(int n) {
this.n = n;
this.keeper = new BitKeeper();
}
public void work() {
for (int i = 0; i < n; i++) {
this.keeper.random();
}
}
public void debug() {
System.out.printf("%d %.2f %d\n", this.n, Math.log(this.n) / Math.log(2), this.keeper.maxbits);
}
}
public static void main(String[] args) {
for (int i = 1000; i < 100000; i += 100) {
Experiment exp = new Experiment(i);
exp.work();
exp.debug();
}
}
}Observing Outputs
Running this will yield outputs like:
36400 15.15 13
36500 15.16 16
...From this experiment, we observe a significant linear correlation between k and n :
If N falls between 2^K and 2^(K+1) , using this method yields an estimated value equal to ( 2^K ), which is clearly unreasonable. To refine our estimate, we can use multiple BitKeeper instances for weighted estimation.
Enhanced Experiment with Multiple Buckets
python
import math
import random
def low_zeros(value):
for i in range(1, 32):
if value >> i << i != value:
break
return i - 1
class BitKeeper:
def __init__(self):
self.maxbits = 0
def random(self, m):
bits = low_zeros(m)
if bits > self.maxbits:
self.maxbits = bits
class Experiment:
def __init__(self, n, k=1024):
self.n = n
self.k = k
self.keepers = [BitKeeper() for _ in range(k)]
def do(self):
for _ in range(self.n):
m = random.randint(0, 1 << 32 - 1)
keeper = self.keepers[((m & 0xfff0000) >> 16) % len(self.keepers)]
keeper.random(m)
def estimate(self):
sumbits_inverse = sum(1.0 / keeper.maxbits for keeper in self.keepers)
avgbits = float(self.k) / sumbits_inverse
return 2 ** avgbits * self.k
for i in range(100000, 1000000, 100000):
exp = Experiment(i)
exp.do()
est = exp.estimate()
print(i, '%.2f' % est, '%.2f' % (abs(est - i) / i))Java Version
Here's the Java equivalent:
java
public class PfTest {
static class BitKeeper {
private int maxbits;
public void random(long value) {
int bits = lowZeros(value);
if (bits > this.maxbits) {
this.maxbits = bits;
}
}
private int lowZeros(long value) {
int i = 1;
for (; i < 32; i++) {
if (value >> i << i != value) {
break;
}
}
return i - 1;
}
}
static class Experiment {
private int n;
private int k;
private BitKeeper[] keepers;
public Experiment(int n) {
this(n, 1024);
}
public Experiment(int n, int k) {
this.n = n;
this.k = k;
this.keepers = new BitKeeper[k];
for (int i = 0; i < k; i++) {
this.keepers[i] = new BitKeeper();
}
}
public void work() {
for (int i = 0; i < this.n; i++) {
long m = ThreadLocalRandom.current().nextLong(1L << 32);
BitKeeper keeper = keepers[(int) (((m & 0xfff0000) >> 16) % keepers.length)];
keeper.random(m);
}
}
public double estimate() {
double sumbitsInverse = 0.0;
for (BitKeeper keeper : keepers) {
sumbitsInverse += 1.0 / (float) keeper.maxbits;
}
double avgBits = (float) keepers.length / sumbitsInverse;
return Math.pow(2, avgBits) * this.k;
}
}
public static void main(String[] args) {
for (int i = 100000; i < 1000000; i += 100000) {
Experiment exp = new Experiment(i);
exp.work();
double est = exp.estimate();
System.out.printf("%d %.2f %.2f\n", i, est, Math.abs(est - i) / i);
}
}
}In the code, we used 1024 buckets, and the average was calculated using the harmonic mean (the average of the reciprocals). This approach is beneficial because the ordinary mean can be significantly affected by outliers, while the harmonic mean effectively smooths the influence of those outliers.
The script's output demonstrates that the error rate is kept within single-digit percentages:
100000 97287.38 0.03
200000 189369.02 0.05
300000 287770.04 0.04
400000 401233.52 0.00
500000 491704.97 0.02
600000 604233.92 0.01
700000 721127.67 0.03
800000 832308.12 0.04
900000 870954.86 0.03
1000000 1075497.64 0.08While the above example provides a decent estimation, the actual HyperLogLog implementation is more complex and precise. One potential issue in this simplified algorithm is that when the random counts are low, it can lead to division by zero errors, as the maximum bits (maxbits) may remain at zero. This is an important consideration for robust implementations where edge cases should be handled properly.
Memory Consumption of pf
In our earlier algorithm, we used 1024 buckets for independent counting. In Redis's HyperLogLog implementation, 16384 buckets (i.e., ( 2^{14} )) are utilized, requiring 6 bits per bucket to store the maximum bits. Thus, the total memory consumption is:
Reflection & Assignment
Try grouping a set of data, counting separately, and then using pfmerge to combine them. Compare the pfcount values with the statistics obtained without grouping to observe any discrepancies.