Bloom Filters ​

In the previous section, we learned to use the HyperLogLog data structure for estimation, which is very valuable for solving many statistical needs with low precision.

However, if we want to know whether a specific value already exists in the HyperLogLog structure, it falls short. It only provides the pfadd and pfcount methods, without a method like pfcontains.

Let’s discuss a use case. When using a news client to read articles, it continually recommends new content, ensuring duplicates are removed. The question arises: how does the recommendation system implement deduplication?

You might think that the server records all historical records of user views. When recommending news, the system filters out content that has already been viewed from each user's history. The problem is that with a large user base and numerous articles viewed by each user, can the deduplication work of the recommendation system keep up in terms of performance?

If the historical records are stored in a relational database, deduplication requires frequent exists queries to the database. When the system faces high concurrency, the database struggles to handle the load.

You may think of caching, but caching all those historical records would waste a lot of storage space. Moreover, this storage space grows linearly over time—if you can manage it for a month, can you sustain it for years? But without caching, performance won’t keep up. What should we do?

This is where the Bloom Filter shines. It is specifically designed to solve deduplication issues. While it performs deduplication, it can also save over 90% of space, with only a slight imprecision, meaning it has a certain probability of false positives.

What is a Bloom Filter? ​

A Bloom Filter can be understood as an imprecise set structure. When you use its contains method to check if an object exists, it may return a false positive. However, it's not completely imprecise; with reasonable parameter settings, its accuracy can be controlled to be sufficiently precise, resulting in only a small probability of false positives.

When a Bloom Filter indicates that a value exists, that value might not actually exist. However, when it says it does not exist, it definitely does not. For example, if it says it doesn’t recognize you, it truly does not. But if it says it has seen you before, it might have never met you; it could just be that your face resembles someone it knows (based on certain familiar face combinations), leading to a false positive.

In the context mentioned earlier, a Bloom Filter can accurately filter out content that has already been viewed, while it may also filter out a very small portion of new content (false positives). However, it can accurately identify the vast majority of new content, ensuring that the content recommended to users is duplicate-free.

Bloom Filters in Redis ​

The official Bloom Filter provided by Redis made its debut with the plugin feature in Redis 4.0. As a plugin, it enhances Redis Server with powerful Bloom deduplication capabilities.

Let’s experience the Bloom Filter in Redis 4.0. To simplify the installation process, we can use Docker.

docker pull redislabs/rebloom  # Pull the image
docker run -p6379:6379 redislabs/rebloom  # Run the container
redis-cli  # Connect to the Redis service in the container

If the above commands execute without issues, we can now try out the Bloom Filter.

Basic Usage of Bloom Filters ​

Bloom Filters have two basic commands: bf.add to add elements and bf.exists to query whether an element exists. Their usage is similar to the sadd and sismember commands for sets. Note that bf.add can only add one element at a time; to add multiple elements, you need to use the bf.madd command. Similarly, if you need to check multiple elements at once, you use bf.mexists.

127.0.0.1:6379> bf.add codehole user1
(integer) 1
127.0.0.1:6379> bf.add codehole user2
(integer) 1
127.0.0.1:6379> bf.add codehole user3
(integer) 1
127.0.0.1:6379> bf.exists codehole user1
(integer) 1
127.0.0.1:6379> bf.exists codehole user2
(integer) 1
127.0.0.1:6379> bf.exists codehole user3
(integer) 1
127.0.0.1:6379> bf.exists codehole user4
(integer) 0
127.0.0.1:6379> bf.madd codehole user4 user5 user6
1) (integer) 1
2) (integer) 1
3) (integer) 1
127.0.0.1:6379> bf.mexists codehole user4 user5 user6 user7
1) (integer) 1
2) (integer) 1
3) (integer) 1
4) (integer) 0

It seems quite accurate with no false positives. Next, let’s use a Python script to add many elements and see at which point the Bloom Filter starts to return false positives.

# coding: utf-8

import redis

client = redis.StrictRedis()

client.delete("codehole")
for i in range(100000):
    client.execute_command("bf.add", "codehole", "user%d" % i)
    ret = client.execute_command("bf.exists", "codehole", "user%d" % i)
    if ret == 0:
        print(i)
        break

The Java client Jedis-2.x does not provide a command extension mechanism, so you cannot directly use Jedis to access the Redis Module's bf.xxx commands. RedisLabs provides a separate package called JReBloom, which is based on Jedis-3.0, but this package has not yet been released to the Maven central repository. If you prefer simplicity, you can use Lettuce, another Redis client that has long supported command extensions compared to Jedis.

public class BloomTest {
    public static void main(String[] args) {
        Client client = new Client();

        client.delete("codehole");
        for (int i = 0; i < 100000; i++) {
            client.add("codehole", "user" + i);
            boolean ret = client.exists("codehole", "user" + i);
            if (!ret) {
                System.out.println(i);
                break;
            }
        }

        client.close();
    }
}

After running the above code, you may be surprised to find that there is no output. After adding 100,000 elements, there are still no false positives. If you try adding another zero, you’ll find that there are still no false positives.

The reason is that a Bloom Filter will never falsely identify an existing element; it only falsely identifies elements that have not been seen. Thus, we need to adjust the script slightly to check for unseen elements using bf.exists, to see if it mistakenly thinks it has seen them.

# coding: utf-8

import redis

client = redis.StrictRedis()

client.delete("codehole")
for i in range(100000):
    client.execute_command("bf.add", "codehole", "user%d" % i)
    # Note i+1; this is the current unseen element
    ret = client.execute_command("bf.exists", "codehole", "user%d" % (i + 1))
    if ret == 1:
        print(i)
        break

The Java version:

public class BloomTest {
    public static void main(String[] args) {
        Client client = new Client();

        client.delete("codehole");
        for (int i = 0; i < 100000; i++) {
            client.add("codehole", "user" + i);
            boolean ret = client.exists("codehole", "user" + (i + 1));
            if (ret) {
                System.out.println(i);
                break;
            }
        }

        client.close();
    }
}

After running this, we see that the output is 214, meaning that at element 214, a false positive occurred.

Measuring the False Positive Rate ​

How can we measure the false positive rate? First, we randomly generate a set of strings and split them into two groups. We then insert one group into a Bloom filter and check if the strings in the other group exist, taking the number of false positives divided by half the total number of strings as the false positive rate.

# coding: utf-8

import redis
import random

client = redis.StrictRedis()

CHARS = ''.join([chr(ord('a') + i) for i in range(26)])

def random_string(n):
    chars = []
    for i in range(n):
        idx = random.randint(0, len(CHARS) - 1)
        chars.append(CHARS[idx])
    return ''.join(chars)

users = list(set([random_string(64) for i in range(100000)]))
print 'total users', len(users)
users_train = users[:len(users)/2]
users_test = users[len(users)/2:]

client.delete("codehole")
falses = 0

for user in users_train:
    client.execute_command("bf.add", "codehole", user)
print 'all trained'
for user in users_test:
    ret = client.execute_command("bf.exists", "codehole", user)
    if ret == 1:
        falses += 1

print falses, len(users_test)

Java version:

public class BloomTest {
    private String chars;
    {
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < 26; i++) {
            builder.append((char) ('a' + i));
        }
        chars = builder.toString();
    }

    private String randomString(int n) {
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < n; i++) {
            int idx = ThreadLocalRandom.current().nextInt(chars.length());
            builder.append(chars.charAt(idx));
        }
        return builder.toString();
    }

    private List<String> randomUsers(int n) {
        List<String> users = new ArrayList<>();
        for (int i = 0; i < 100000; i++) {
            users.add(randomString(64));
        }
        return users;
    }

    public static void main(String[] args) {
        BloomTest bloomer = new BloomTest();
        List<String> users = bloomer.randomUsers(100000);
        List<String> usersTrain = users.subList(0, users.size() / 2);
        List<String> usersTest = users.subList(users.size() / 2, users.size());

        Client client = new Client();
        client.delete("codehole");
        for (String user : usersTrain) {
            client.add("codehole", user);
        }
        int falses = 0;
        for (String user : usersTest) {
            boolean ret = client.exists("codehole", user);
            if (ret) {
                falses++;
            }
        }
        System.out.printf("%d %d\n", falses, usersTest.size());
        client.close();
    }
}

After running this for about a minute, you should see:

total users 100000
all trained
628 50000

The false positive rate is about 1% or so. You might wonder if this rate is still a bit high; is there a way to lower it? The answer is yes.

Using Custom Parameters for Bloom Filters ​

The Bloom filter we used above has default parameters, created automatically when we first add items. Redis also provides custom parameter Bloom filters, which require explicit creation using the bf.reserve command before adding items. If the corresponding key already exists, bf.reserve will throw an error. The bf.reserve command takes three parameters: key, error_rate, and initial_size. A lower error rate requires more space. The initial_size parameter indicates the estimated number of elements to be stored; exceeding this number will increase the false positive rate.

Therefore, it’s essential to set a larger estimate to avoid exceeding it, which can lead to a higher false positive rate. By default, the error_rate is 0.01, and the initial_size is 100.

Next, let’s modify the script using bf.reserve:

# coding: utf-8

import redis
import random

client = redis.StrictRedis()

CHARS = ''.join([chr(ord('a') + i) for i in range(26)])

def random_string(n):
    chars = []
    for i in range(n):
        idx = random.randint(0, len(CHARS) - 1)
        chars.append(CHARS[idx])
    return ''.join(chars)

users = list(set([random_string(64) for i in range(100000)]))
print 'total users', len(users)
users_train = users[:len(users)/2]
users_test = users[len(users)/2:]

falses = 0
client.delete("codehole")
# Added this line
client.execute_command("bf.reserve", "codehole", 0.001, 50000)
for user in users_train:
    client.execute_command("bf.add", "codehole", user)
print 'all trained'
for user in users_test:
    ret = client.execute_command("bf.exists", "codehole", user)
    if ret == 1:
        falses += 1

print falses, len(users_test)

Java version:

public class BloomTest {
    private String chars;
    {
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < 26; i++) {
            builder.append((char) ('a' + i));
        }
        chars = builder.toString();
    }

    private String randomString(int n) {
        StringBuilder builder = new StringBuilder();
        for (int i = 0; i < n; i++) {
            int idx = ThreadLocalRandom.current().nextInt(chars.length());
            builder.append(chars.charAt(idx));
        }
        return builder.toString();
    }

    private List<String> randomUsers(int n) {
        List<String> users = new ArrayList<>();
        for (int i = 0; i < 100000; i++) {
            users.add(randomString(64));
        }
        return users;
    }

    public static void main(String[] args) {
        BloomTest bloomer = new BloomTest();
        List<String> users = bloomer.randomUsers(100000);
        List<String> usersTrain = users.subList(0, users.size() / 2);
        List<String> usersTest = users.subList(users.size() / 2, users.size());

        Client client = new Client();
        client.delete("codehole");
        // Corresponding to the bf.reserve command
        client.createFilter("codehole", 50000, 0.001);
        for (String user : usersTrain) {
            client.add("codehole", user);
        }
        int falses = 0;
        for (String user : usersTest) {
            boolean ret = client.exists("codehole", user);
            if (ret) {
                falses++;
            }
        }
        System.out.printf("%d %d\n", falses, usersTest.size());
        client.close();
    }
}

After running this for about a minute, the output should be:

total users 100000
all trained
6 50000

We see a false positive rate of about 0.012%, much lower than the expected 0.1%. However, the probability of Bloom filters can vary; as long as it does not exceed the expected rate significantly, it's acceptable.

Considerations ​

If the Bloom filter's initial size is overestimated, it wastes storage space; if underestimated, it impacts accuracy. Users must estimate the element count as accurately as possible and add some buffer space to avoid significantly exceeding the estimate.

The smaller the error rate, the more storage space is required. In cases where high precision is not necessary, setting a slightly larger error rate can be acceptable. For instance, in news deduplication, a higher false positive rate only means that a few articles may not be seen by the right audience, but it won't drastically change the overall readership.

The Principle of Bloom Filters ​

Having learned to use Bloom filters, it’s essential to explain the underlying principle to avoid leaving readers in the dark.

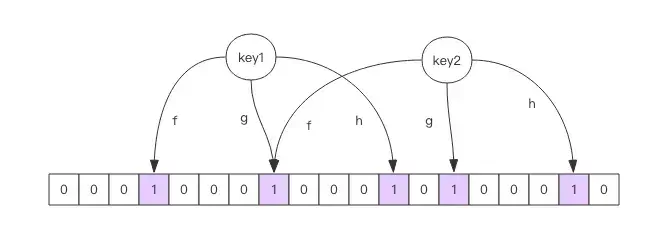
Each Bloom filter corresponds to a large bit array and several unbiased hash functions in Redis. "Unbiased" means that it distributes the hash values fairly evenly.

When adding a key to the Bloom filter, multiple hash functions calculate an integer index for the key, which is then modded by the length of the bit array to get a position. Each hash function yields a different position. The specified bit array positions are then set to 1, completing the add operation.

To check if a key exists, the same hash positions are calculated. If any bit is 0, the key does not exist in the Bloom filter. If all are 1, the key likely exists, but this could be due to other keys also being present. If the bit array is sparse, the accuracy of the check increases; if it's crowded, accuracy decreases. The specific probability calculations are complex, and if interested, readers can explore further, but it can be quite challenging.

During usage, ensure that the actual elements do not significantly exceed the initialized size. When the number of actual elements starts to exceed this size, the Bloom filter should be rebuilt, allocating a larger size and batch adding all historical elements (this requires storing all historical elements elsewhere).

Since the error rate does not spike dramatically when the number exceeds the estimate, this provides a lenient timeframe for rebuilding the filter.

Space Occupancy Estimation ​

The space occupancy of a Bloom filter can be calculated using a simple formula, though the derivation is quite complex, so we'll skip it here. Interested readers can refer to "extended reading" for a deeper understanding.

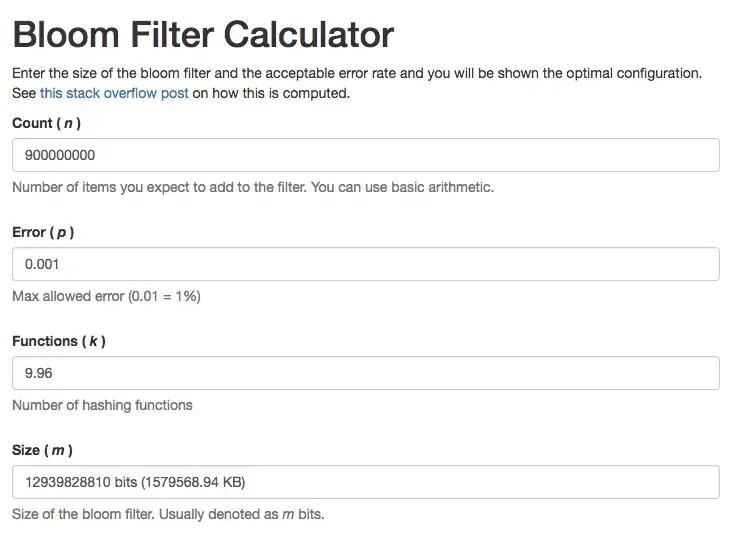
A Bloom filter has two parameters: the estimated number of elements n and the error rate f . The formula provides two outputs: the length of the bit array l , representing the required storage size (in bits), and the optimal number of hash functions k . The number of hash functions directly impacts the error rate, with the optimal number yielding the lowest rate.

k=0.7*(l/n) 
f=0.6185^(l/n)

From these formulas, we can see:

• As the bit array length relative to n increases l/n , the error rate f decreases, which is intuitive.
• A longer bit array requires a larger optimal number of hash functions, affecting computational efficiency.

For example, when each element averages 1 byte (8 bits) of fingerprint space l/n = 8 , the error rate is approximately 2%. Other examples include:

• Error rate of 10%: average fingerprint space of about 5 bits.
• Error rate of 1%: average fingerprint space of about 10 bits.
• Error rate of 0.1%: average fingerprint space of about 15 bits.

You may wonder if a requirement of 15 bits per element diminishes the space advantage over a set. However, it's essential to note that a set stores the content of each element, while a Bloom filter only stores fingerprints. The actual size of each element can range from several bytes to hundreds, and each element requires a pointer in the set, taking up 4 or 8 bytes depending on whether the system is 32-bit or 64-bit. Thus, the space advantage of Bloom filters remains significant.

For those who find the calculations cumbersome, many websites offer tools to compute space occupancy by inputting parameters, such as the Bloom Calculator.

Impact of Actual Elements Exceeding Estimates on False Positive Rate ​

When the actual number of elements exceeds the estimated number, how much does the error rate change? Does it spike dramatically or rise gradually? This can be described using another formula, introducing a parameter t to represent the ratio of actual elements to estimated elements:

f=(1-0.5^t)^k

As t increases, the error rate f also increases. We can choose k values for error rates of 10%, 1%, and 0.1% to plot the curves for visual observation.

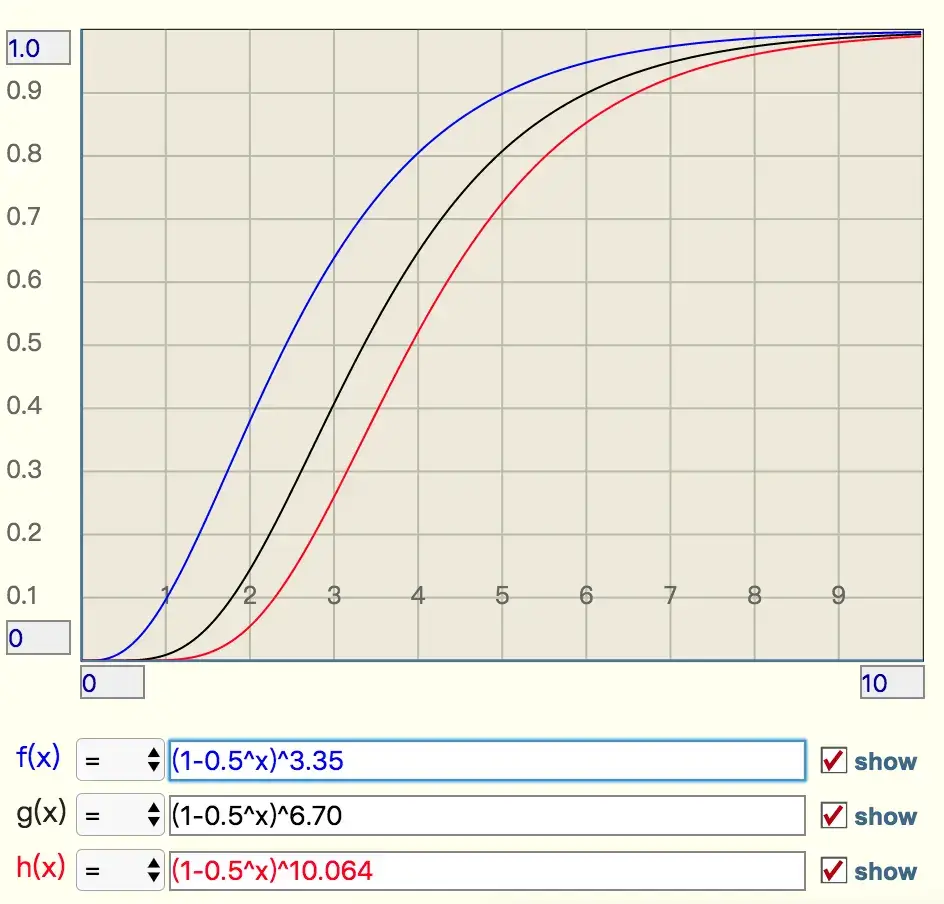
The curves indicate a steep rise:

• For an error rate of 10%, when the ratio is 2, the error rate approaches 40%, which is quite dangerous.
• For an error rate of 1%, when the ratio is 2, the error rate rises to 15%, which is concerning.
• For an error rate of 0.1%, when the ratio is 2, the error rate reaches 5%, which is also risky.

What If You Can't Use Redis 4.0? ​

Before Redis 4.0, there were third-party Bloom filter libraries that implemented a Bloom filter using Redis bitmaps, but their performance is considerably lower. For example, a single exists query may involve multiple getbit operations, resulting in higher network overhead. Additionally, these third-party libraries are not perfect; for instance, the pyrebloom library does not support reconnection and retries, requiring additional layers of encapsulation for production use.

• Python Redis Bloom Filter
• Java Redis Bloom Filter

Other Applications of Bloom Filters ​

In web crawling systems, Bloom filters can be used to deduplicate URLs. With millions or even billions of URLs, storing them in a set can be extremely space-inefficient. A Bloom filter can significantly reduce storage consumption for deduplication, albeit at the cost of potentially missing a few pages.

Bloom filters are widely used in NoSQL databases, such as HBase, Cassandra, LevelDB, and RocksDB, where they help reduce the number of I/O requests. When querying a specific row, a Bloom filter in memory can quickly filter out many non-existent row requests before accessing the disk.

Email systems also commonly employ Bloom filters for spam filtering. While this helps in reducing false positives, some legitimate emails may occasionally end up in the spam folder, albeit at a low probability.