Turtle Graphics | Ucode

Appearance

On this page

Turtle Graphics ​

In 1966, Seymour Papert and Wally Feurzig invented a programming language designed for children called LOGO. Its hallmark feature is commanding a small turtle to draw on the screen through programming.

Turtle Graphics was later adapted to various high-level languages, and Python includes the turtle library, which essentially replicates 100% of the original Turtle Graphics functionality.

Let’s look at a simple code example that commands the turtle to draw a rectangle:

python
# Import everything from the turtle package:
from turtle import *

# Set brush width:
width(4)

# Move forward:
forward(200)
# Turn right 90 degrees:
right(90)

# Set brush color:
pencolor('red')
forward(100)
right(90)

pencolor('green')
forward(200)
right(90)

pencolor('blue')
forward(100)
right(90)

# Call done() to make the window wait to be closed; otherwise, it will close immediately:
done()

When running this code in the command line, a drawing window will automatically pop up and a rectangle will be drawn:

rect.webp

From the program code, we can see that turtle graphics involve directing the turtle to move forward and turn. The path the turtle takes forms the drawn lines. To draw a rectangle, we just need to make the turtle move forward and turn right 90 degrees, repeating this four times.

The width() function sets the brush width, while the pencolor() function sets the color. For more operations, please refer to the documentation of the turtle library.

After completing the drawing, remember to call the done() function to let the window enter the message loop and wait to be closed. Otherwise, the Python process will terminate immediately, causing the window to close right away.

The turtle package itself is just a drawing library, but combined with Python code, it can create various complex shapes. For example, drawing five stars using a loop:

python
from turtle import *

def drawStar(x, y):
    pu()
    goto(x, y)
    pd()
    # Set heading: 0
    seth(0)
    for i in range(5):
        fd(40)
        rt(144)

for x in range(0, 250, 50):
    drawStar(x, 0)

done()

The execution result of the program looks like this:

stars.webp

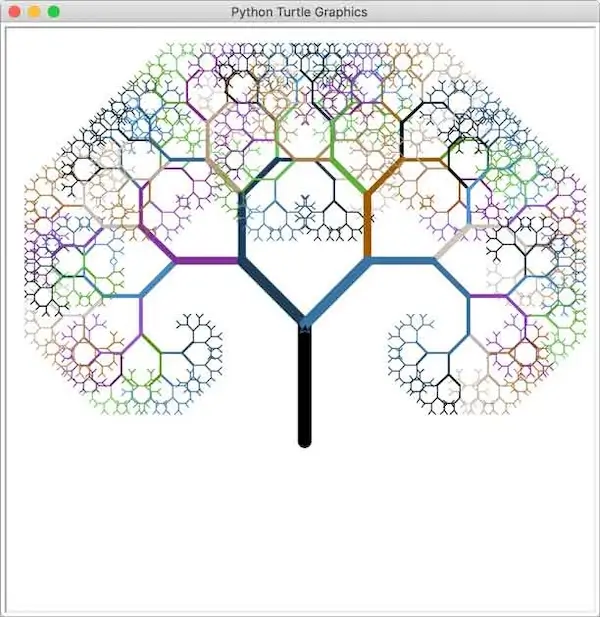
Using recursion, we can draw very complex shapes. For instance, the following code can draw a fractal tree:

python
from turtle import *

# Set color mode to RGB:
colormode(255)

lt(90)

lv = 14
l = 120
s = 45

width(lv)

# Initialize RGB colors:
r = 0
g = 0
b = 0
pencolor(r, g, b)

penup()
bk(l)
pendown()
fd(l)

def draw_tree(l, level):
    global r, g, b
    # Save the current pen width
    w = width()

    # Narrow the pen width
    width(w * 3.0 / 4.0)
    # Set color:
    r = r + 1
    g = g + 2
    b = b + 3
    pencolor(r % 200, g % 200, b % 200)

    l = 3.0 / 4.0 * l

    lt(s)
    fd(l)

    if level < lv:
        draw_tree(l, level + 1)
    bk(l)
    rt(2 * s)
    fd(l)

    if level < lv:
        draw_tree(l, level + 1)
    bk(l)
    lt(s)

    # Restore the previous pen width
    width(w)

speed("fastest")

draw_tree(l, 4)

done()

Executing this program takes some time, and the final effect looks like this:

tree.webp